
Осторожно, это видео может «вынести» вам мозг.
Смотрите, я вас предупредил.
«Вынос мозга» проводит Александр Сергеев — научный журналист, член комиссии РАН по борьбе со лженаукой.
Так как у амеб нет ничего даже отдалённо напоминающего центральную нервную систему, это делает их наименее подходящими кандидатами для решения задач такой сложности. Тем не менее, японские исследователи обнаружили, что некоторые виды амёб можно использовать в качестве своеобразных «процессорных модулей» для биокомпьютеров будущего…
«Группа исследователей из Университета Кейо в Токио доказала, что амеба способна решать знаменитую «задачу коммивояжера» и при определенных условиях может обогнать по скорости вычислений компьютер.
Необычайно умное существо называется Physarum polycephalum (дословный перевод с латинского языка «многоголовая слизь«).
«Physarum polycephalum уже использовалась ранее в качестве биологического компьютера в нескольких других экспериментах. Данное существо считают особенно полезным в биологических вычислениях, потому что она может расширять различные области своего тела в поисках более эффективного способа получения пищи, и она ненавидит свет.
Чтобы превратить этот естественный механизм питания в компьютер, японские исследователи поместили амёбу на специальную пластину с 64 каналами, в направлении которых животное могло вытягивать тело. Амёба постоянно пытается расширить тело, чтобы покрыть как можно большую площадь пластины с питательным веществом. Тем не менее, каждый канал в пластине можно осветить, что заставляет амебу из чувства отвращения к свету убраться из этого канала.
Для моделирования задачи коммивояжера каждому из 64 каналов на табличке был присвоен код города между A и H, в дополнение к номеру от 1 до 8, который указывает порядок городов (порядок городов соответствует порядку их посещения коммивояжёром).
Для программирования амёбы исследователи использовали нейронную сеть, которая включала данные о текущем положении амебы и расстоянии между городами, чтобы осветить определённые каналы. Нейронная сеть была обучена с большей вероятностью освещать города (каналы) с бóльшими расстояниями между ними.
При взаимодействии алгоритма и амёбы последняя принимает форму, которая представляет приблизительные решения задачи коммивояжера. Самое интересное, что количество времени, которое требуется амёбе для получения этих почти оптимальных решений, растёт линейно, хотя количество вариантов решения увеличивается экспоненциально. В ближайшее время исследователи собираются изготовить чипы с десятками тысяч каналов, чтобы амёба могла попробовать решить задачу коммивояжера на сотнях городов.»
«Решения «задачи коммивояжера», полученные вычислительной системой на основе амёбы.
Примеры туров коммивояжёра по четырём, пяти, шести, семи и восьми городам, полученные в экспериментах,
где каждый тур окрашен в красный цвет на соответствующих каналах с правого рисунка.
Левые панели показывают переданные светлые изображения начальных состояний»
«Выяснилось, что микроорганизм почти всегда решает эту задачу идеально точно. И скорость принятия решений увеличивается линейно при усложнении задачи, хотя в IT-науке рост вычислительных операций в этом случае должен расти по экспоненте. Это трудно объяснить с позиции науки, поэтому эксперименты продолжаются. Сейчас заказаны пробирки с архитектурой для имитации десятков тысяч объектов-кормушек – интересно наблюдать за поведением амебы при таком лавинообразном усложнении условий задачи.
Ученые пока не совсем поняли механизм, благодаря которому одноклеточному организму удается выбрать кратчайший маршрут, но, если удастся поставить на службу науке таких вот амеб, возможно, они помогут пересмотреть подход не только к существующим алгоритмам вычисления, но и к компьютерным системам безопасности, считают исследователи.»
Научная статья опубликована 19 декабря 2018 года в журнале Royal Society Open Science (doi: 10.1098/rsos.180396).
Для справки:
Задача коммивояжёра (англ. Travelling salesman problem, сокращённо TSP) — одна из самых известных задач комбинаторной оптимизации, заключающаяся в поиске самого выгодного маршрута, проходящего через указанные города хотя бы по одному разу с последующим возвратом в исходный город. В условиях задачи указываются критерий выгодности маршрута (кратчайший, самый дешёвый, совокупный критерий и тому подобное) и соответствующие матрицы расстояний, стоимости и тому подобного. Как правило, указывается, что маршрут должен проходить через каждый город только один раз — в таком случае выбор осуществляется среди гамильтоновых циклов. Существует несколько частных случаев общей постановки задачи, в частности, геометрическая задача коммивояжёра (также называемая планарной или евклидовой, когда матрица расстояний отражает расстояния между точками на плоскости), метрическая задача коммивояжёра (когда на матрице стоимостей выполняется неравенство треугольника), симметричная и асимметричная задачи коммивояжёра. Также существует обобщение задачи, так называемая обобщённая задача коммивояжёра.
Оптимизационная постановка задачи относится к классу NP-трудных задач, впрочем, как и большинство её частных случаев. Версия «decision problem» (то есть такая, в которой ставится вопрос, существует ли маршрут не длиннее, чем заданное значение k) относится к классу NP-полных задач. Задача коммивояжёра относится к числу трансвычислительных: уже при относительно небольшом числе городов (66 и более) она не может быть решена методом перебора вариантов никакими теоретически мыслимыми компьютерами за время, меньшее нескольких миллиардов лет.
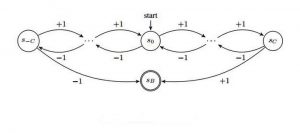
Два математика из Ливерпульского университета, Великобритания, Алексей Лисица и Борис Конев, придумали интересную проблему – если компьютер приводит доказательство математической задачи, которое слишком велико для изучения, то как судить, насколько оно верное?
В своей статье, учёные описывают написание и запуск компьютерной программы для решения малой части задачи, известной как задача несоответствия Эрдеша.
Конечно, математиков терзали смутные сомнения, что когда-нибудь, в один из не самых прекрасных дней, компьютер будет работать очень долго, а результат его работы будет очень велик.
Результат работы программы Лисицы и Конева поражает воображение – файл с текстом доказательства занимает объём в 13 гигабайт, т.е. 13,000,000,000 Байт!
Это на два гигабайта больше, чем полный объём информации в Википедии.
Теперь перед научным миром стоит дилемма: либо принимать на веру доказательства, созданные машинами, как факт (хотя мы не в состоянии их проверить), либо отказаться от их использования, ограничивая тем самым наши возможности.

Антрополог поинтересовался, как он пришел к такому выводу.
— Разумеется, я всё доказал математически, — ответил абориген.
— Я завязал на веревке два узелка, затем завязал ещё два узелка на другой веревке. А когда я связал обе верёвки вместе, у меня получилось пять узелков.
Для справки:
Математика — фундаментальная наука, предоставляющая (общие) языковые средства другим наукам; тем самым она выявляет их структурную взаимосвязь и способствует нахождению самых общих законов природы.
Доказательство — рассуждение по определенным правилам, обосновывающее какое-либо утверждение.
Логическое доказательство — логическая операция обоснования истинности утверждения с помощью фактов и связанных с ним суждений. С помощью совокупности логических приёмов истинность какого-либо суждения обосновывается исходя из других истинных суждений.
Математическое доказательство — рассуждение с целью обоснования истинности какого-либо утверждения (теоремы), цепочка логических умозаключений, показывающая, что при условии истинности некоторого набора аксиом и правил вывода утверждение верно.